void Duplicate(NoodOp*,NoodOp**)
создает точную копию заданного дерева
void FuseTreeP2(NoodOp*) ставит затычку в
ответвление P2 дерева.
void HideTreeP1 HideTreeP2(NoodOp*)
тоже самое, но само поддерево физически не уничтожается.
void ExpandSet(NoodOp*) избавляет дерево от операций
между множествами, заменяя
их логическими конструкциями. Возможно я буду это использовать, при вычислениях.
Хотя проверяя принадлежность буквы пересечению множеств, я все равно не стал бы
пересекать множества, а играл бы только с проверяемой буквой. Если точнее, оперируя
набором из 16 множеств. Можно составить таблицу WORD[256], ячейки которой
должны своими битами указывать какому множеству буква принадлежит, а какому нет.
А сложное выражение (A1\A2)\(A3\A4)U(A6\A9) можно заменить двумя битовыми масками,
которые говорят о том какому множеству символ должен принадлежать, а какому нет.
И натыкаясь на подобное выражение, просто накладывать обе маски на элемент массива.
void LinearTree(NoodOp*) выполняет разбалансировку
дерева. Т.е. делает так, чтобы
одна операция не осуществлялась между результатами себе подобных. Кроме того ставит в
конце каждой зоны заглушку. Этот фокус упрощает многие операции над деревом.
Не затрагиваются операции со множествами, и им подобные. При перераспределении операций
'+', '-' из знак изменяется.
void OrderTree(NoodOp*) сортирует разбалансированое
дерево. (не разбалансированое дерево будет приведено в хаос).
void CanonTree(NoodOp*) пытается привести два дерева
к одинаковому виду.
Таким образом деревья представляющие собой одинаковые формулы, приводятся
к одинаковому виду, в случае если они не выражены по разному. Эти преобразования позволяют
сравнивать два дерева, не прибегая к сложной процедуре сравнения.
void WipeTree(NoodOp**) обходит дерево и очищает его,
от так называемых заглушек. Которые остаются после некоторых преобразований.
Основная проблема в том,
что после некоторых действий в программе возникают фальшивые зоны.
char ifCoincedesTree(NoodOp*, NoodOp*)
сравнивает два преобразованных дерева.
Возвращает ноль, если они равны.
И разницу между несовпадающими элементами в противном случае.
Процедура ищет разницу между деревьями в следующем порядке : имя узла;
затем если это операнд, то аргумент; если операция, то поддерево p2, затем p1.
bool ifContainsZone(NoodOp*, NoodOp*)
возвращает истину если первая зона является частным случаем второй зоны.
Если зоны не состоят из логических операций, то возвращает результат прямого сравнения.
bool ifDualCoincedesTree(NoodOp *tree1, NoodOp *tree2)
сравнивает два дерева. Возвращает истину, если деревья являются, противоположными
логическими операциями, над одинаковыми операндами.
void ExludeZone(NoodOp*,NoodOp*, char new)
находит и удаляет элементы первой зоны из второй зоны.
Если второе дерево операция, то эта операция уничтожается без, какого либо анализа.
new операнд которым нужно заместить уничтоженные элементы.
bool FindAtom(NoodOp*,AtomsName,char)
ищет заданную терминальную вершину в дереве. Возвращает истину если она там есть.
bool SimplifySum(NoodOp*)
попытка упростить суммы записанные в дереве. Для заданного узла: если он является
суммой двух чисел, то числа складываются. Если данная операция минус, то в ответвлении
p1 ищется такой же операнд с плюсом, если он найден, то происходит сокращение слагаемых.
Процедура расчитанна на разбалансированное дерево. И в принципе вовсе не нужна.
Работает только с текущим узлом.
Суммы которые ответвляются от данного узла не рассматривает.
bool FactorTree(NoodOp*)
находит общий множитель в логических выражениях и выносит его за скобки.
Вложенные выражения не проверяются.
bool RemoveIdentical(NoodOp*)
Для заданной логической операции, пытается найти в поддереве такой же логический
операнд и уничтожить его.
Принцип следующий : X1 | X2 | X3 если X2 содержит X1, то в X2 вместо X1 можно
подставить false, потому как для значения true X2 все равно не будет востребовано.
X1 ^ X2 ^ X3 в X2 вместо X1 можно подставить true, т.к. при false выражение
все равно не сработает.
bool RemoveIdenticalSub1(NoodOp*, NoodOp*)
ищет и уничтожает элементы первого дерева в элементах второго поддерева второго дерева.
bool RemoveDual(NoodOp*)
Реализует следующее преобразование :
(μ=1 | μ≠1 ^ ξμ-1='5') → (μ=1 ^ ξμ-1='5')
принцип тот же, что и в предыдущей ситуации, но в X2 ищется
противоположное условие.
Условие {a 0 n} (ξa≠ 'у') преобразуется в так
называемый коньюктивный цикл. Цикл считается истиной, если при переборе всех его значений
в его теле не возникало лжи. Моя мысль проста до идиотизма : вытащить из тела цикла все
что не зависит от его параметра.
Чтобы все процедуры работы с деревом были универсальны параметры цикла хранятся в виде
набора обычных узлов :
{a 3 c} (ξa='5')
bool OpenCycle(NoodOp**)
вытягивает из цикла логические операнды не зависящие от переменной цикла.
Может полностью уничтожить цикл, если это необходимо.
bool JustifyCycle(NoodOp*)
изменяет границу цикла, если она контролируется в теле цикла
... ...
...
О, И, Е, А, H, Т, C, В, Р, Л, К, Д, М, П, У, Ы, Я, Б, Г, З, Ь,
Ч, Х, Ж, Ш, Ю, Ц, Щ, Э, Ф,
CТ, HО, ЕH, ТО, HА, ОВ, HИ, РА, ВО, КО, ОИ, ИИ, ИЕ, ЕИ, ОЕ, ИЯ,
HH, CC,
CТО, ЕHО, HОВ, ТОВ, ОВО, HАЛ, РАЛ, HИC.
1
/ 1
--[^] 3 /
\ / --[^]
[^] \
\ [Fuse]
6
x ~ A1 U A2 = x ~ A1 | x ~ A2
x ~ A1 @ A2 = x ~ A1 & x ~ A2
x ~ A1 \ A2 = x ~ A1 & x $ A2
x $ A1 U A2 = x $ A1 & x $ A2
x $ A1 @ A2 = x $ A1 | x $ A2
x $ A1 \ A2 = x $ A1 | x ~ A2
x1 x1 [fuse]
/ / /
[^] [^] [^]
/ \ / \ / \
/ x2 [^] x2 [^] x1
[^] / \ / \
\ x3 [^] x4 [^] x2
\ / \ / \
[^] x3 [^] x4
\ \
x4 x3
1 1
/ /
[-] 2 [+]
\ / / \
[-] [-] 3
\ \
3 2
1-(2-3)=1-2+3 1-2+3
void CanonTree(NoodOp *tree)
{
LinearTree(tree);
OrderTree(tree);
}
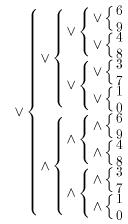 →
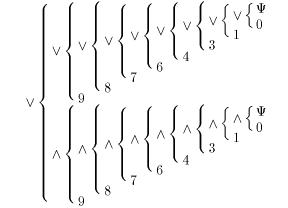
→ 
/
[^]
/
[^] [Fuse]
/ \ /
[^] [|]
/ \ /
[^]
/
[Fuse]
/
[Fuse] [|]
/ / \
[|] [|] X3
/ \ / \
-[|] X3 -[|] X2
\ \
X1 X1
X1 X1
/ /
-[=] -[≠]
\ \
X2 X2
Первое Второе Результат
?
/ ? ?
?-[?] \ \
\ [3] [Fuse]
?
/ [^] [^]
[^] / \ / \
/ \ [^] [9] [^] [Fuse]
-[^] [9] / \ / \
\ -[^] [3] -[^] [3]
[1] \ \
[1] [Fuse]
X1
/
-[^] X2 arg = 3
\ / AtomsName = num
[|]
\
3
Now terrible
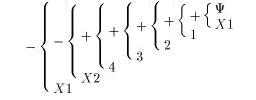 →
→ 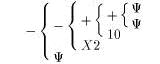
(A ^ B) | (A ^ C) = A ^ ( B | C)
(A | B) ^ (A | C) = A | ( B ^ C)
X3 X3 X3
/ / /
[^] [^] [^]
/ / /
-[^] X1 -[^] X1 -[^] X1
\ / \ / \ /
[|] X2 [|] X2 [|]
\ / \ / \
[^] [^] X2
\ \
X3 True
[...] [RemoveIndentical] [Wipe]
для анализа и изменения используются процедуры ifContainsZone, ExludeZone.
[=] [=]
/ /
-[|] [≠] -[|] True
\ / \ /
[^] [^]
\ \
We go further
[a 0 n] (X1(a) ^ X2) = X2 ^ [a 0 n] (X1(a))
[a 0 n] (X1(a) | X2) = X2 | [a 0 n] (X1(a))
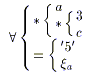
[a,0,b] X1
/ /
-[Cycle] X1 -[|] [a,0,b]
\ / \ /
[|] a [Cycle] a
\ / \ /
[=] [=]
\ \
3 3
[a,0,b]
/ 1
-[Cycle] 1 /
\ / -[=]
[=] \
\ b
b
[a,1,b]
/ [a,2,b]
-[Cycle] X1 /
\ / -[Cycle] X1
[^] 1 \ /
\ / [^]
[=] \
\ [Fuse]
a
Планы (чтоб не забыть)
Взаимная оптимизация правил
...
Оптимизация с учетом вероятности
Статистика
Частота бyкв/бyквосочетаний в рyсском языке:
Относительная частота