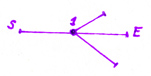
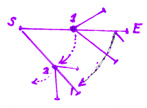
Предположим что у нас есть какая-то текстовая строка. S,E - начало и конец нашей строки.
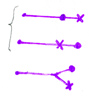
Посмотрим на самую длинную ветку нашего суффикного дерева. Схематично её можно изобразить так:

Теперь представим другие ветки нашего дерева. Допустим мы отрезали нашего текста первый символ.
В этом случае на дереве мы получим точно такую же ветку, но более короткую (более короткое начало).
Поскольку составляя дерево мы всегда отрезаем этот символ, то обе такие ветки есть в нашем дереве:
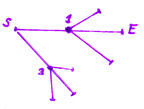
и обе эти ветки не отличаются ничем кроме длины. У веток разумеется может быть похожий начальный отрезок, в таком случае разветвление может быть не в корне дерева, а чуть дальше.
Теперь появляется такое понятие, как суффиксная связь. В суффиксные связи, связывают все похожие ветки дерева.
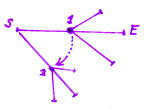
В нашем примере суффиксная связь первой ветки указывает на более короткую копию.
Cуффиксная связь второй ветки указывает на следущую ещё более короткую копию:
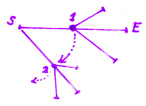
Вершины 1 и 2 стоят на разном расстоянии от корня. Если суффиксная связь связывает две вершины, то глубина этих вершин всегда отличается только на один символ (это думаю очевидно).
Теперь Алгоритм Укконена. Суть его в том что наш тектовой отрезок растёт, а вместе в ним растёт суффиксное дерево, которое мы имеем. Наша строка S, E вырастает на один символ.Для того чтобы обновить дерево, достаточно просто наложить на неё новую более длинную строку. От этого наложения измениться одна из веток дерева, а это изменение мы сможем раскопировать по всему дереву, используя наши суффиксные связи.
Теперь представим что может происходить в тот момент, когда ты складываем два текстовых отрезка:

Условно возможны две ситуации. Либо наши отрезки одинаковые (не считая разной длины), тогда ничего не меняется.
Либо один из символов различается, в результате чего создаётся развилка.
Теперь представим наше дерево. Если мы добавили новый символ. То все концы у дереве вырастут на один символ. Кроме того на кончиках дерева могут появиться новые развилки, но эти развилки всегда будут небольшие, и всегда будут появляться только у самых кончиков дерева (потому что все предыдущие символы мы не меняли).
Суть (и вся красота) Алгоритма Укконена, которая отличает его от всех похожих алгоритмов, состоит в том - что добавляя новый символ к строке, мы выращиваем наше дерево. А для этого он всего лишь проверяем в нём возможность возникновения новых развилок, которую создаёт новый символ строки (больше делать ему ничего не надо). Простыми словами: если мы добавляем символ, то алгоритм берёт этот (и только этот) символ и просто делает одно сравнение (в одном только месте). Сравнивает его c тем местом где может появиться первая развилка. Больше он не делает ничего. Если новый символ создаёт развилку, то она появляется, затем таким же образом проверяются все копии этого места, для чего достаточно пробежать по суффиксным связям от того места где появилась первая развилка.
Создание новых суффиксных связей: поскольку все копии вновь появившейся развилки, будут абсолютно одинаковыми, по пути все вновь созданные развилки будут связанны между собой новой суффиксной связью.
up. файл устарел. попозже выложу новый, предельно понятный исходник