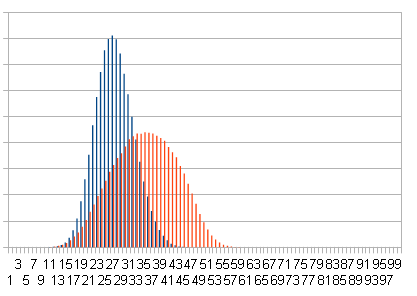
Синим - результат вставки случайных чисел. Красным - вставка отсортированных чисел.
std::string RandLine(FILE *f)
{
std::vector<std::string>text; // все строчки текста
for(int count=0; !feof(f); count++) text.push_back(ReadLine(f));
if(!count) return "";
return text[rand()%count];
}
|
Способ второй, нормальный. Смотрим на вероятность выдачи каждой строки. Если в тексте одна строка, то она будет выбрана с вероятностью 1. Если две строки, то одна из них выбирается с вероятностью 1/2. Если три строки, то 1/3 и т.д. Небольшая доделка и мы получаем процедуру, которая с одинаковой вероятностью выдаёт любую строку файла, при этом не загружает текст в память:
std::string RandLine(FILE *f)
{
std::string res;
for(int count=1; !feof(f); count++)
{
std::string line=ReadLine(f);
if(rand()%count==0) res=line;
}
return res;
}
|
struct Node{
int v;
Node *p1,*p2;
int count; // число узлов ветки, включая текущий
Node(int v):v(v),p1(0),p2(0),count(1) { }
int Count() const { this?count:0; }
void FixCount() { size=1+p1->FixCount()+p2->FixCount(); }
};
|
Node* Insert(Node *node,int v)
{
if(!node || rand()%(node->count+1)==0) return InsertRoot(node,v); // p=1/(count+1)
if(v < node->v) node->p1=Insert(node->p1,v);
else node->p2=Insert(node->p2,v);
node->count++;
return node;
}
|
InsertRoot - вставка узла в корень ветки. Её можно написать по разному. В оригинале она выглядит вот так:
Node* InsertRoot(Node *node,int v)
{
Node *n=new Node(v);
Split(node,&n->p1,&n->p2,v);
n->FixCount();
return n;
}
void Split(Node *node,Node **p1,Node **p2,int v)
{
if(!node) {*p1=*p2=0;return;}
if(v < node->v) *p2=node, Split(node->p1,p1,&node->p1,v);
else *p1=node, Split(node->p2,&node->p2,p2,v);
node->FixCount();
}
|
Кое где упоминается вариант, который работает через вращение:
Node* InsertRoot(Node *node,int v)
{
if(!node) return new Node(v);
if(v < node->v)
{
node->p1=InsertRoot(node->p1,v);
return Rotate21(node);
}
else
{
node->p2=InsertRoot(node->p2,v);
return Rotate12(node);
}
}
[more]
Node* Rotate12(Node *node)
{
Node* p2=node->p2;
node->p2=p2->p1;
p2->p1=node;
p2->count=node->count;
node->FixCount();
return p2;
}
Node* Rotate21(Node *node)
{
Node* p1=node->p1;
node->p1=p1->p2;
p1->p2=node;
p1->count=node->count;
node->FixCount();
return p1;
}
|
Не смотря, на вроде бы разный смысл, оба варианта эквивалетны, т.е. делают одно и тоже. Поэтому проще использовать второй вариант, но после некоторого упрощения. Заодно можно избавиться от неприятных двойных ссылок.
Node *InsertRoot(Node *node, int v)
{
Node *q;
if(!node) return new Node(v);
if(v < node->v)
{
q=InsertRoot(node->p1,v);
node->p1=q->p2, q->p2=node; // Rotate21
}
else
{
q=InsertRoot(node->p2,v);
node->p2=q->p1, q->p1=node; // Rotate12
}
q->count=node->count+1;
node->FixCount();
return q;
}
|
см.: rand-tree.cpp - ссылки в конце
Node *Remove(Node *node,int v)
{
if(!node) return 0;
if(v < node->v) node->p1=Remove(node->p1,v);
else if(v > node->v) node->p2=Remove(node->p2,v);
else
{
Node *d=node;
node=Join(node->p1,node->p2);
delete d;
}
if(node) node->FixCount();
return node;
}
Node *Join(Node *p1,Node *p2)
{
if(!p1) return p2;
if(!p2) return p1;
if(rand()%(p1->count+p2->count) < p1->count) // p=m/(n+m)
{
p1->p2=Join(p1->p2,p2);
p1->FixCount();
return p1;
} else {
p2->p1=Join(p1,p2->p1);
p2->FixCount();
return p2;
}
}
|

Синим - результат вставки случайных чисел. Красным - вставка отсортированных чисел.
Разброс длин довольно ощутимый, но тем не менее мы не уступаем по скорости любому другому алгоритму балансировки. Было бы ещё лучше, если бы мы могли избавиться от счётчика вершин внутри каждого узла, и от вызова rand(). Потому что rand() довольно медленная процедура, и вызывать её из каждого узла очень расточительно. Избавиться от node->count было ещё интереснее. Во первых так мы экономим память, во вторых не придётся пересчитывать это число вдоль всего пути. К сожалению убрать его просто так нельзя, потому что надо рассчитывать вероятности. Если вращать дерево наугад, то оно быстро вырождается.
Кстати этот самый node->count можно использовать напрямую, без всяких случайностей. Просто смотреть на него после добавления вершины, и поворачивать узлы, там где один count перевешивает другой. Получается некоторый аналог AVL дерева.
В рандомизированном дереве это сделать просто. А даже если бы это было не так, не обязательно строго следить за структурой веток. Поэтому мы можем не только сделать удаление за один вызов, мы можем просто выдрать из дерево любой количество произвольных вершин. Дерево само приведёт себя к рабочему состоянию.
Кроме того для рандомизированных деревьев, есть все операции, которые можно делать со множествами. Есть замечательные и простые алгоритмы: слияния, объединения, вычитания, пересечения и симметричной разности. Правда до состояния рабочего кода их надо немного доработать (на это пока не хватало времени).
1: 1000000 - корень 2: 499999 - левая и правая ветка 3: 249999 4: 124999 5: 62499 .... 36: 9 37: 8 38: 7 39: 7 40: 6 41: 5 42: 5 ... 57: 1 - листы 58: 1 59: 1 60: 1 61: 1Проще говоря мы можем убрать node->count и заменить его каким-то статическим числом. На практике это конешно очень грубое допущение, и разброс чисел среди узлов одного уровня, как правило огромный. Но работает это всё таки неплохо:
Node* Insert(Node *node,int v,int count)
{
if(!node || rand()%count==0) return InsertRoot(node,v); // p=1/(count+1)
count=count/2+1;
if(v<node->v) node->p1=Insert(node->p1,v,count);
else node->p2=Insert(node->p2,v,count);
return node;
}
void Insert(int v)
{
count++;
root=Insert(root,v,count);
}
|
Для удаления, на нужно чем-то заменить вероятность p=m/(m+n) в процедуре Join. Поскольку узлы p1 и p2 всегда находятся на одной высоте, то можно сделать такое допущение: p=m/(m+n)=1/2. На самом деле p зависит от высоты, но не очень сильно. Вообще от того насколько точно мы учитываем вероятность, зависит ширина горба на гистограмме (см. любую картинку). Если погрешность у формулы большая, то горб будет немного шире, а алгоритм немного хуже. С другой стороны ничто не даёт такой хороший прирост скорости, как простота.
Node *Join(Node *p1,Node *p2)
{
...
if(rand()%2) {
p1->p2=Join(p1->p2,p2);
return p1;
} else {
p2->p1=Join(p1,p2->p1);
return p2;
}
}
|
Таким образом мы получаем упрощённую версию версию рандомизированного дерева. Баланс узлов как правило у него немного хуже:
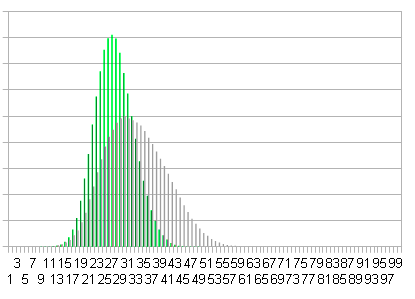
Зелёным - длины путей в нормальном рандомизированном дереве. Серым - длины путей в упрощённом дереве.
Но ухудшение баланса не так плохо влияет на скорость. В зависимости от характера данных, упрощенное дерево может работать как быстрее, так и медленнее оригинального.
Примеру если заталкивать в дерево отсортированные числа, то оно сработает в несколько раз быстрее, даже по сравнению со своим оригиналом.
Поэтому на большом количестве данных, применять его следует осторожно. Вырождаться дерево всё таки не будет, но в некоторых случаях оно может слегка замедляться.
Сразу оговорю, что эффекта, от самой экономии памяти, вы можете не заметить, потому что память запросто сожрёт родной new, delete c++ в результате выравнивания.
Если польза от этой экономии всё таки нужна, то придётся использовать свой распределитель памяти, или найти какое-то применение для свободного места внутри узлов.
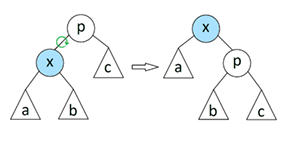
Для того чтобы выдернуть узел в корень, мы поднимаемся от заданного узла в корень, и выполняем банальную цель поворотов. Подъём по дереву выполняется шагами, по два узла. Применяются две операции: так называемое Zig-Zig преобразование, и Zig-Zag преобразование.
На примерах, x - это узел, заданный для подъёма к корню (подкрасил его голубым); g - текущий родительский узел (никак его не покрасил, где он потом окажется - не важно).
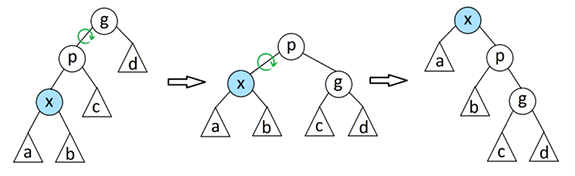
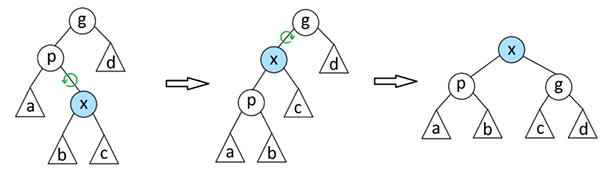
Шагать к корню ровно по одной вершине, и делать повороты - очевидно, нельзя. Дерево после таких манёвров, мгновенно станет списком.
Поэтому делаем два шага, применяем одну из показанных операций,
делаем ещё два шага, и так пока не попадём к корню. Само собой, путь до корня может состоять из нечётного числа шагов. В это случае, в конце пути, вершина не доберется до корня, останется ниже на одни уровень.
В этой ситуации, мы делаем один маленький окончательный поворот, вокруг корня (Zig операция). Да, тут не самые удачные рисунки (не нашёл у кого своровать более удачные):
Главный недостаток - полная зависимость от входных данных. Стоит засунуть в него простой набор возрастающих чисел, или даже запросить последовательность возрастающих чисел, и Splay превращается в банальный плоский список. Тут оно ничего не отличается от небалансируемово дерева. Конечно, если потом я подёргаю дерево случайными запросами, то нормальная структура восстановится, но не так быстро как портится. Выглядит это странно. На первый взгляд, с такими свойствами, с тем же успехом, можно применять не балансируемое дерево, и от Splay оно ничем отличаться не будет.
К тому же, первая фантазия, которая приходит в голову. Можно применять то же не балансируемое дерево, но для для сравнения использовать хеши, от наших чисел. Баланс будет отличный. Будет не хуже любого случайного дерева, только быстрее и проще.
Полноценного решения проблемы, плохого баланса в Splay деревьях нету!
Коротко говоря, есть специфичные проблемы, и нет идеального решения. Всё решается по вкусу.