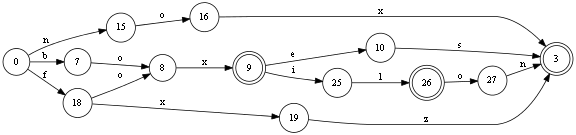
- двойными кружками обозначены концы слов:
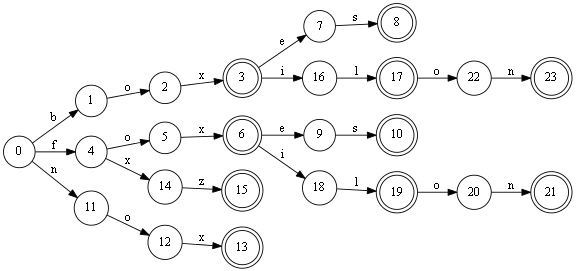
Мы же будем склеивать одинаковые начальные и конечные отрезки слов. Т.е строить минимальный ациклический граф, для словаря или проще говоря даг.
Выглядит это примерно так:

- двойными кружками обозначены концы слов:
Отмечу основные моменты:
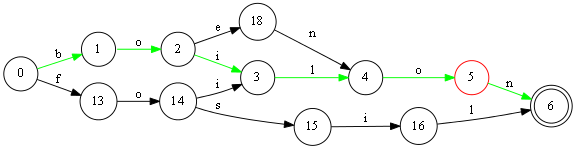
допустим мы добавляем что-то очень похожее на слово boilon и на вершине номер 5 у нас возникает новое ответвление. Просто так добавить эту ветку мы не можем,
потому что по пути к этой вершине у нас содержится целых три слова [boilon, foilon, foenon], они будут затронуты при любом изменении.
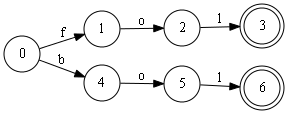
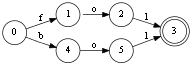
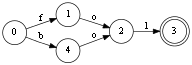
Перед тем как что-то изменять мы должны оторвать от графа путь со словом boilon и выделить его в отдельную ветку:
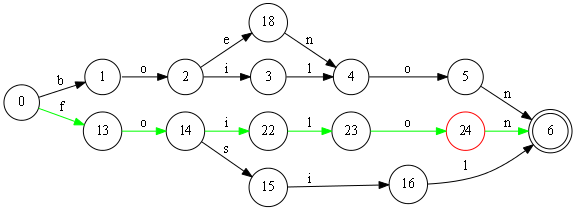
Для такого отделения достаточно найти вдоль пути первую вершину, у которой есть две или больше входящих дуг (у нас это вершина номер 3). Разорвать эту дугу и построить полную копию остального пути.
При этом вершины которые идут после вершины номер 5 отслаивать(копировать) уже не нужно, на них наша новая ветке никак не влияет.
 |  |
 |  |  |
Найти и слить одинаковые деревья очень просто. Делается это начиная с конца, для каждой вершины на надо найти похожую на неё, и исправить все ссылки. Вершины считаются похожими, если они ссылаются на один и тот же набор узлов и имеют похоже содержимое. В нашем случае никакого содержимого нет, кроме признака конца слова. При этом не надо сравнивать узлы рекурсивно. Если мы уже обработали дочерние узлы дерева, то одинаковые ветки узла уже станут одной вершиной. В нашем случае мы даже не сливаем никаких похожих деревьев, нам просто надо пройтись вдоль одного пути от конца к началу.
struct State{
uint id; // идентификатор
bool fin; // флаг конца слова
uint in; // количество дуг, входящих в узел
}
|
Для работы с узлом используется несколько простых операций:
State{
bool empty() const; // проверка на пустоту (не исходящих связей из узла)
bool is(char sym) const; // проверить, есть ли исходящая связь по данному символу
bool eq(const State *s) const; // сравнить узел с заданным узлом
void set(char sym,State *to); // установить связь по заданному символу
void del(char sym); // удалить связь по заданному символу
State *get(char sym) const; // получить связь по заданному символу
}
|
Пара вспомогательных классов:
Очень важно поддерживать корректый счётчик входящих дуг для узлов. А также корректную хеш таблицу, т.е. вовремя добавлять и удралять из неё узлы. С тем чтобы там небыло потеряных узлов,
были актуальные, и были только нужные в данный момент. К примеру если, во время добавления я буду делать обновления не совсем в нужный момент, то в графе могут появиться циклы или ещё какие гадости.
Например к слову deon я добавил denton, и достаточно чуть чуть ошибится с обномление хеша, чтобы у нас вместо хорошего графа, получится плохой:

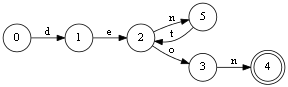
Ещё пара вспомогательных процедур:
void Add(const char *txt)
{
Split(0,txt); // отслоение
Add(0,txt);
}
void Del(const char *txt)
{
Split(0,txt); // отслоение
Del(0,txt);
}
|
void Merge(State *st,State *st1,char sym) // слияние
{
State *st2=reg.Get(st1);
if(st2) {
SetLink(st,sym,st2);
reg.Del(st1);
DelState(st1);
}
}
|
Всё удаление и добавление делается рекурсивно. Т.е. предполагается что в работе будут всё таки настоящие слова, которые совсем не бесконечны. А рекурсивная процедура возвращает либо само дерево (граф), либо её его копию со вновь создаными элементами. Т.е. всё работает в чистом духе функционального программирования. На самом деле это не совсем так, но очень близко к истине и переделка под какой-то нибудь реально функциональный язык будет вполне выполнимой задачей. К тому же это позволило до безобразия упростить сами процедуры. Я совместил всем процедуру добавления и слияния. А сами процедуры добавления и удаления оказались настолько похожими водяными каплями, что их наверное можно заменить одной общей процедурой. Разницы между ними я выделил:
State *Del(State *st,const char *txt)
{
char sym=*txt++;
reg.Del(st); // удаление из хеш таблицы
if(sym) {
if(!st->is(sym)) return st;
State *s=Del(st->get(sym),txt);
SetLink(st,sym,s);
Merge(st,s,sym);
}else st->fin=false;
if(st->empty() && !st->fin) {
DelState(st); // удаление узла
return 0;
}
reg.Add(st); // добавление в хеш таблицу
return st;
}
|
State *Add(State *st,const char *txt)
{
char sym=*txt++;
reg.Del(st);
if(sym) {
State *s;
if(st->is(sym)) s=Add(st->get(sym),txt);
else s=Add(NewState(),txt);
SetLink(st,sym,s);
Merge(st,s,sym);
} else st->fin=true;
reg.Add(st);
return st;
}
|
st->hide=true;
uint hash1=st->Hash();
...
st->hide=false;
uint hash2=st->Hash();
if (hash1!=hash2) {
reg.Del(hash1,st);
reg.Add(hash2,st);
}
|
State *Split(State *st,const char *txt,bool dup)
{
if(st→in>1) dup=true;
if(dup) st=DupState(st); else reg.Del(st);
char sym=*txt++;
if(!sym) return st;
State *s=st→get(sym);
if(!s) return st;
SetLink(st,sym,Split(s,txt,dup));
return st;
}
|