Красно-чёрное дерево (RB-дерево)
Красно-черные деревья предложил Д.Байер, назвав их симметричными двоичными Б-деревьями. Л.Гибас подробно изучил их свойства и предложил использовать для наглядности красный и черный цвета
(год точно не помню, кажется 74-й или где-то рядом).
Про них написано почти везде. Поэтому подробно рассказывать я ничего не буду.
Постараюсь только написать чуть красивее, короче и ближе к делу.
Для того чтобы прочитать это вы должны уметь работать с бинарными деревьями поиска.
Основы
- Каждая вершина имеет цвет: красный или чёрный.
- У красной вершины оба потомка всегда чёрные.
- В любом пути дерева всегда одинаковое количество чёрных вершин.
Дополнения
- Корень дерева всегда чёрный.
- Нулевая ссылка принимается за чёрную вершину, которая имеет чёрных потомков.
Капля теории
Извиняюсь что схемы набраны текстом, уже небыло сил рисовать как надо.
Как упомянуто выше, RB дерево на самом деле имитирует B-дерево, каждый узел которого имеет не более 4-х потомков.
Соотвествия приблизительно следующие:
| B-узел | RB-узлы | тройки RB-узлов
|
(1)
/
a
|
(1)
/
a
|
|
. (1) .
/
a
|
(1)
/ \
a b
|
(1)
/ \
a b
|
|
. (1) .
/ \
a b
|
(1) (2)
/ | \
a b c
|
(1)
/ \
(2) c
/ \
a b
|
|
(2)-(1) .
/ \ \
a b с
|
(1) (2) (3)
/ | | \
a b c d
|
(1)
/ \
(2) (3)
/ \ / \
a b c d
|
|
(2)-(1)-(3)
/ \ / \
a b c d
|
Таким образом, если путь до каждого листа в дереве имеет одинаковое число чёрных вершин, то соотвествующее отображение в B-дерево, имеет одинаковую
глубину листьев, как и положено B-дереву. Т.е. каждый узел B-дерева содержит один черный узел, и один, два красных по краям.
Обозначения на рисунках:
- Серые вершины, это вершины цвет которых не имеет значения.
- Стрелка показывает направление поворота.
- Красный крестик показывает вершину, которую удалили (по мере подьёма по дереву, обозначание начинает носить условный характер).
- 'R' локальный корень той конструкции в дереве, с которой мы работаем в текущее мгновение.
Не знаю как описан данный алгоритм в оригинале, возможно не совсем так, как у меня. Я написал это как мог.
Вставка
Находим в дереве место для вставки, вставляем узел красного цвета.
Поднимаемся вверх по дереву и находим ситуации, которые условно можно обозначить так:
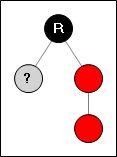
Не важно что и куда вставлено, надо просто найти в дереве нужные шаблоны.
Ситуация 1:
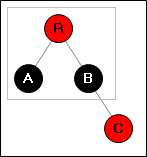
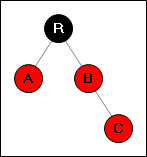 →
→ 
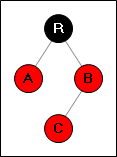 →
→ 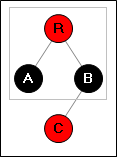
Просто перекрашиваем три вершины (R,A,B).
Ситуация 2:
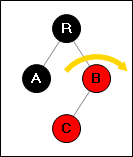 →
→ 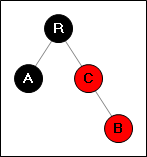
Выполняем маленький поворот без перекраски вершин.
Ситуация 3:
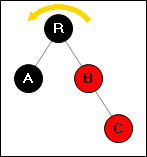 →
→ 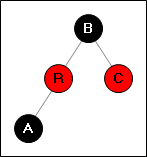
Перекрашиваем две вершины (R,B) и выполняем поворот.
Удаление
Почти такие-же по смыслу действия. Находим вершину которую надо удалить (назовём её A). Если вершину нельзя удалить сразу, находим вершину
которую можно вставить на место удаляемой (назовём её B). Замена при этом окрашивается в цвет удалённой вершины (B красится в цвет A).
Далее мы смотрим цвет той вершины, которую мы убрали физически (если была замена, то смотрим цвет вершины B).
Теперь рассматриваем ситуации возникающие на дереве (крестиком пометили вершину, которая была убрана):
Ситуация 0:
Если была убрана красная вершина, перекрашиваем её в чёрную.
Прекращаем работу.
Ситуация 1:
Удалённая вершина имеет красного брата.
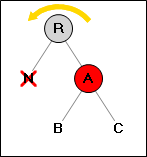 →
→ 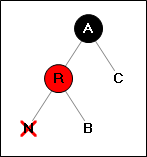
Перекрашиваем две вершины (A,R). Делаем поворот. Выполняем повторую проверку ситуаций для вершины (C),
если для неё была применена ситуация 2, красим (C) в чёрный цвет.
Прекрашаем работу.
Ситуация 2:
Удалённая вершина имеет чёрного брата с чёрными потомками.
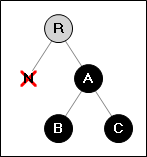 →
→ 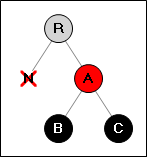
Перекрашиваем вершину (A) в чёрный цвет.
Продолжаем работу, над вершиной выше по дереву.
Ситуация 3:
Удалённая вершина имеет чёрного брата, у которого красный левый и чёрный правый потомок.
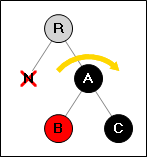 →
→ 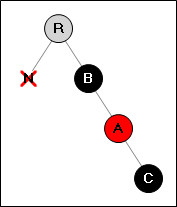
Перекрашиваем вершины (A,B). Поворачиваем вершину (A).
Сразу же, переходим в проверке ситуации 4.
Ситуация 4:
Удалённая вершина имеет чёрного брата, у которого красный правый потомок (цвет левого потомка брата тут не важен).
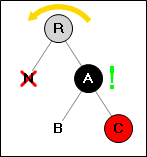 →
→ 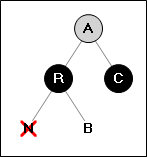
Перекрашиваем вершину (A) в цвет вершины (R). Перекрашиваем вершины (R,C) в черный цвет.
Делаем поворот.
Прекращаем работу.
Детали
Чтобы сократить проверки на нулевые ссылки при работе, во время вставки и удаления, можно ввести фиктивную нулевую вершину.
Фиктивная вершина окрашена в чёрный цвет. Её указатели на левые и правые поддеревья, ссылаются на неё же.
Ссылка на фиктивную вершину - считается нулевой ссылкой.
В принципе код, этот трюк не сильно упрощает (особенно если не нужны процедуры удаления).
Но беглые тесты показывают, что при интенсивной работе со вставкой и удалением, такое дерево работает несколько быстрее.
Важный совет
Большая часть кода дерева, это удаление узла. Если вы работаете только на добавление, то исходник будет в несколько раз меньше.
Если вы делаете дерево для которого предусмотренно только добавление узлов: не делайте тупость, и не создавайте внутри узлов ссылки на родителький узел.
Она попросту там не нужна:
- всё отлично работает без неё
- она поедает много лишней памяти
- она попросту очень усложняет код и служит потенциальным источником ошибок
Даже если вы пишете полный код с удалением узлов, даже в этом случае (при сильном желании) можно оботись без ссылки на родительский узел
(хотя тут ссылка код всё таки упрошает).
Исходник
Опять же разумеется код можно оптимизировать сильнее, но я не стал
жертвовать остатками наглядности.
Aвтограф =)
(c) Proteus
icq: 133575351
email: lawnmower-man@mail.ru

 →
→ 
 →
→ 
 →
→ 
 →
→ 
 →
→ 
 →
→ 
 →
→ 
 →
→ 