Балансировка бинарного дерева поиска (AVL)

В сбалансированном AVL дереве, фактор баланса для узла T, может принимать одно из трёх значений:

• 0 - ветки 1 и 2 имеют одинаковую высоту.
• -1 - ветки 1 на еденицу выше чем ветка 2
• +1 - ветки 2 на еденицу выше чем ветка 1

Если после вставки или удаления узла, разница между высотами веток, в каком-либо из узлов стала больше 1, то требуется сбалансировать данный узел, повернув данный узел.

→

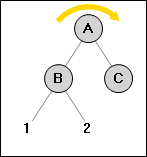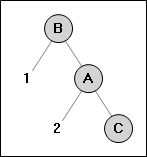
Здесь высота дерева B была больше высоты дерева C, что мы исправили с помощью поворота. Перед выполнением поворота следуется убедится что высота ветки 1 больше высоты ветки 2 (в узле B). Если это не так (например мы вставили узел в ветку 2 узла B), то это следует исправить с помощью предварительного поворота узла B (назовём это вложенный поворот).

Фактор баланса

Tree

→

Tree'

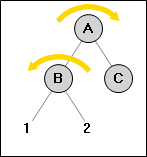
Для исправления фаторов баланса в подобной ситуации, достаточно знать факторы баланса двух вершин перед поворотом, и исправить значения этих же вершин после поворота. Сами значения проще всего описать в табличной форме. Не важно, делаем мы при этом основной или вложенный поворот. Если мы делаем внешний поворот, то предполагается что внутрений уже выполнен. Так же предополагается что фактор баланса лежит в границах от -2 до +2, AVL дереве других факторов быть не может, даже во время временного дисбаланса.

Для вложенного поворота до после A=-1 B=-1 A'=+1 B'=+1 A=-1 B=+0 A'=+1 B'=+0 A=-1 B=+1 A'=+2 B'=+0

Для внешнего поворота до после A=-2 B=-1 A'=+0 B'=+0 A=-2 B=-2 A'=+0 B'=+1 A=-2 B=+0 A'=+1 B'=-1

Процедуры

Структурка узла

struct node_st{ node_st *p1; // левая ветка node_st *p2; // правая ветка int value; // значение узла int b; // фактор баланса };

Поворот вершины слева направо.

node_st *Rotate12(node_st *node) { static const int array[6][4]={ -1,-1,+1,+1, -1,+0,+1,+0, -1,+1,+2,+0, -2,-1,+0,+0, -2,-2,+0,+1, -2,+0,+1,-1 }; node_st *p1=node->p1; node_st *p12=p1->p2; p1->p2=node; node->p1=p12; for(int n=0;n<6;n++) if(array[n][0]==node->b && array[n][1]==p1->b) { p1->b=array[n][2]; node->b=array[n][3]; break; } return p1; }

Поворот вершины cправа налево.

node_st *Rotate21(node_st *node) { static const int array[6][4]={ +1,-1,-2,+0, +1,+0,-1,+0, +1,+1,-1,-1, +2,+0,-1,+1, +2,+1,+0,+0, +2,+2,+0,-1 }; node_st *p2=node->p2; node_st *p21=p2->p1; p2->p1=node; node->p2=p21; for(int n=0;n<6;n++) if(array[n][0]==node->b && array[n][1]==p2->b) { p2->b=array[n][2]; node->b=array[n][3]; break; } return p2; }

Сама процедура баланса

bool BalanceInsert(node_st **root) { node_st *node=*root; if(node->b>1) { if(node->p2->b<0) node->p2=Rotate12(node->p2); *root=Rotate21(node); return true; } if(node->b<-1) { if(node->p1->b>0) node->p1=Rotate21(node->p1); *root=Rotate12(node); return true; } return false; }

Добавление узла

node_st *tree_root=0; // корень дерева Insert(value,&tree_root); // вставка значения в дерево bool Insert(int value,node_st **root) { bool res=false; node_st *node=*root; if(!node) { *root=NewItem(value); return true; } if(value==node->value) return false; if(value<node->value) res=Insert(value,&node->p1) && !!--node->b; else res=Insert(value,&node->p2) && !!++node->b; if(BalanceInsert(root)) res=false; return res; }

Удаление узла

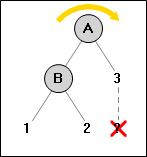
Мы удалили узел из ветки 3, и нам требуется поворот. В это ситуации, если баланс узла B равен нулю, то высота ветки A, после его балансировки не изменится. Для примера можете рассмотреть следующие упрощённые деревья (x - только что удалённая вершина).

    0         0        0
   / \       / \      / \
  1   x     1   x    1   x
 / \       /          \
2   3     2            2

Балансировка после удаления

bool BalanceRemove(node_st **root,bool res) { node_st *node=*root; if(node->b>1) { res=!!node->p2->b; if(node->p2->b<0) node->p2=Rotate12(node->p2); *root=Rotate21(node); } if(node->b<-1) { res=!!node->p1->b; if(node->p1->b>0) node->p1=Rotate21(node->p1); *root=Rotate12(node); } return res; }

Сама процедура удаления

bool Remove(node_st **root,int value)
{
	bool ok=false;
	node_st *node=*root;
	if(!node) return ok;
	if(node->value<value) {
		if(Remove(&node->p2,value) && !--node->b) ok=true;
	}else if(node->value>value) {
		if(Remove(&node->p1,value) && !++node->b) ok=true;
	}else {					// нашли вершину кот. надо удалить
		if(!node->p2) {           	// если есть возможность вырезать сразу, вырезаем
			*root=node->p1;DelItem(node);
			return true;
		}
		ok=GetMin(&node->p2,root);   	// находим вершину, которую вставляем на место удалённой
		(*root)->b =node->b;		// ставим нашу замену на место удалённой вершины
		(*root)->p1=node->p1;
		(*root)->p2=node->p2;
		DelItem(node);
		if(ok) ok=!--(*root)->b;
	} 
	return BalanceRemove(root,ok);
}

Изьятие минимального элемента из ветки дерева

bool tree::GetMin(node_st **root,node_st **res)
{
	node_st *node=*root;
	if(node->p1) {
		if(GetMin(&node->p1,res) && !++node->b) return true;
		return BalanceRemove(root,false);
	}
	*res=node;
	*root=node->p2;
	return true;
}

Файлы

• avl-tree.cpp - первая версия нового балансированного дерева поиска (AVL). Процедуры удаления после вставки и балансировки были сведены к одной процедуре, но суть осталась прежней.
• avl-tree-lite.cpp - тоже самое, но вырезано почти всё без чего можно обойтись. Короче краткая версия.
• avl-tree-nor.cpp - недоделанный вариант. Не рекурсивная версия. Работает только добавление. Остальное доделывать лень.
• Был немного более элегантный нерекурсивный вариант, но я его где-то потерял.

Aвтограф =)