up. текущее дополнение. Понимание самого принципа работы алгоритма, пришло только спустя какое-то время. Сейчас я могу его передать. Но я пока тут будет только старый текст, с механическим описанием действий.
Доминаторы в графе
Итак. Для начала что такое доминаторы. Для вершины в графе, доминатор это ближайшая в нему вершина, через которую проходят все пути идущие в эту вершину.
Ниже нарисовано два примера.
Граф обозначен толстыми линиями, пунктирные стрелки показывают ссылки на доминаторы вершин:
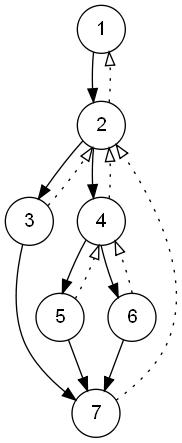
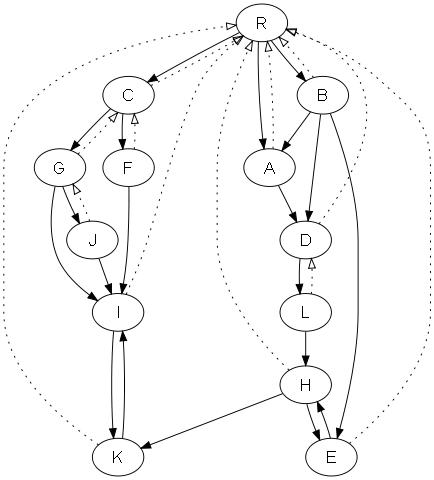
Поиск
Теперь без теорий, определений и очень грубо, на пальцах попытаюсь объяснить как находят доминаторы. Сначала для примера возмём какой-нибудь граф.
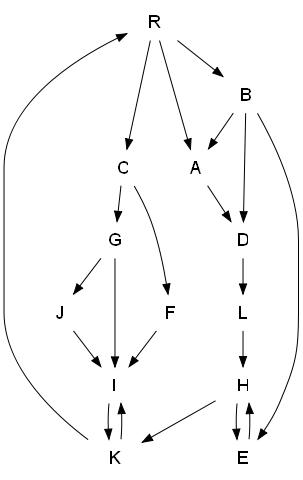
Шаг первый (нумерованное дерево)
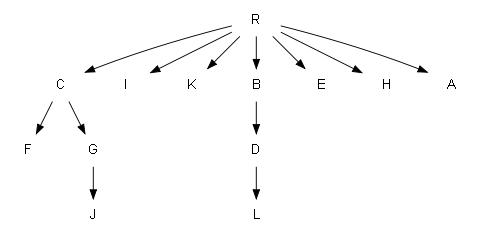
Обходим граф в глубину, нумеруя по пути вершины, т.е. делая из него дерево с пронумероваными вершинами (R - мы приняли за корень дерева):
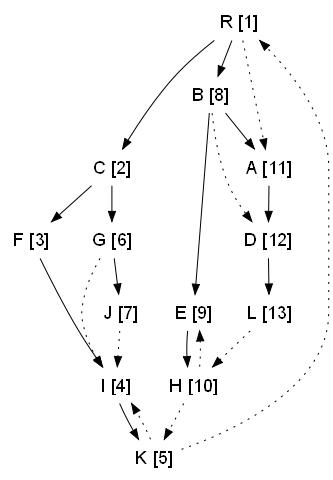
Шаг второй (семидоминаторы)
Находим так называемые семидоминаторы. Когда я буду говорить что одна вершина больше другой и буду имеет виду номера этих вершин.
Так вот, семидоминатор вершины - это минимальная вершина, из которой есть путь в эту вершину, при условии что все вершины
этого пути больше этой вершины (путь может быть пустым, т.е. эта минимальная вершина соеденена с нашей напрямую).
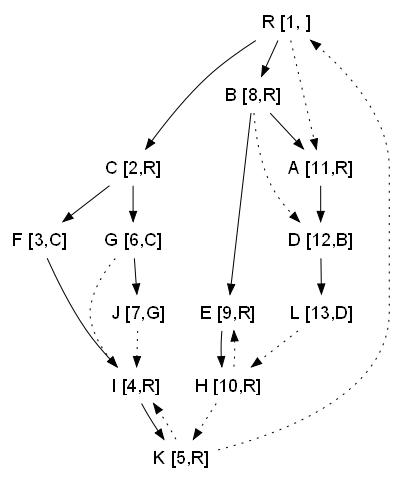
Это легко увидеть на примере ниже. В квадратных скобках указаны семидоминаторы вершин. Рядом нарисовано дерево семидоминаторов.
Пути помеченые пунктиром, всё ещё считаются путями.
Например для E=9, семидоминатором является R=1, поскольку она минимальная, а путь
к ней проходит через большие вершины (A=11 D=12 L=13 H=10).
Тут, вполне очевидно, что из R в E можно попасть разными путями. Т.к. есть путь A, D, L, H, и мы прошли по нему после того как посетили R, E. Будет время - обязательно объясню почему весь этот алгоритм работает.
Шаг третий (доминаторы)
Делаем доминаторы из семидоминаторов. Для этого мы исследуем пути от семидоминатора каждой вершины до неё самой. Если вдоль этого пути нам попадётся вершина
с меньшим семидоминатором, то мы поставим этот семидоминатор в вершину. Например для D=12 - семидоминатором является B=8, но на пути
от B до D, есть вершина A чей семидоминатор меньше, поэтому мы заменяем семидоминатор вершины D на новый (R).
Выполнив все эти коректировки мы получим настоящее дерево доминаторов:
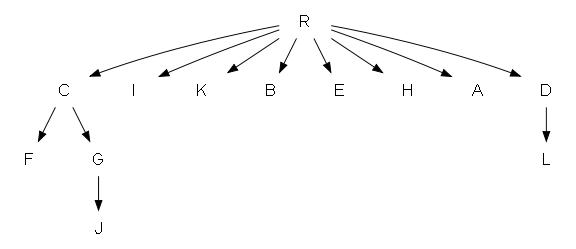
исходный граф и его доминаторы:
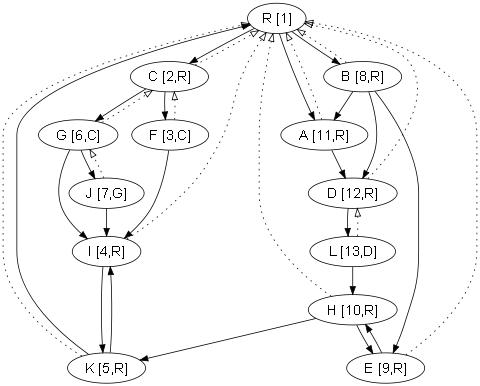
...
Вобщем эти три шага это вся суть алгоритма поиска. Есть на самом деле много разных алгоритмов, но суть у них точно такая же -
все они лишь приукрашенная версия этого алгоритма, структура данных которая ускоряет процесс, порой полностью линейная по времени, и нету в них ничего такого что нельзя было бы придумать самому.
Т.е. любые шаги этого алгоритма можно не хитрым образом ускорить или совместить друг с другом.
К слову, первый шаг линеен по времени; а второй шаг можно вычислять инкрементально, если проверять вершины в порядке убывания номеров.
Только отдельный интерес представляют алгритмы которые позволяют удалить или добавить новое ребро в граф., делая очень быстрый пересчёт доминаторного дерева,
но их я пока описывать не буду.
- dominator.cpp - очень медленный пример, который иллюстрирует весь процесс.
хотя в общем-то не такой уж медленный, надо только доступ к списку рёбер ускорить и разметку всего графа в циклах убрать (например вместо меток ставить id итерации).
(c) Proteus 3:25 02.02.2010









