Array-tree

Введение

Все наверное знают что такое бинарное дерево поиска. Всё очень просто, большие элементы направо, маленькие налево, получаем дерево.

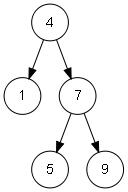
тут любой ребёнок справится: 

struct node_st{char value; node_st *p1,*p2;}*root=0;

void insert(char value)
{
	node_st *node,**p=&root;
	while(node=*p) p=(node->value>value)? &node->p1: &node->p2;
	*p=node=new node_st;
	node->value=value;
	node->p1=node->p2=0;
}

node_st *find(char value)
{
	node_st *node=root;
	while(node) {
		if(node->value==value) break;
		node=(node->value>value)? node->p1: node->p2;
	}
	return node;
}


for(int n=0; n<5; n++) insert("41759"[n]);

У этой системы есть недостатки: 1) ест относительно много памяти, на каждый символ выделяется по структуре. 2) не слишком быстро работает с этой памятью, большой разброс данных.

Сама структура узла дерева имеет размер 12 байт. В хороших компиляторах в зависимости от устройства распределителя памяти на неё будет тратится 16 или 32 байта. Что будет в Visual studio 2003 и выше, я даже думать не хочу, там распределитель был просто убран и отсутсвует полностью. Если написать собсвенный распределитель, но это мало поможет, либо будет 16 байт на структуру, либо выраванивать их придётся по 12 или 9 байт (если упаковать char).

Изменения

Мелкая мысль которая пришла ко мне в голову, когда я делал самодельные множества. Запихнуть в один узел побольше данных. Мы просто запихиваем в каждый узел массив чисел, а сами массивы можно повесить на дерево, так же как обычные числа. В принципе тут ничего сложного, но для нормальной поддержки структуры в рабочем состоянии пришлось ввести некоторые ограничения.


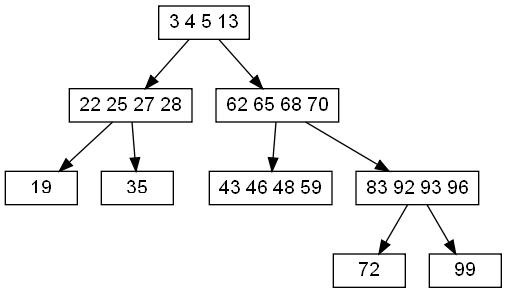
Каждый узел дерева содержит сортированный массив. Если в нём есть свободное место мы вставляем новое число, если надо спускаемся вниз под дереву и работаем с ниже стоящими узлами. При работе с таким деревом, есть только одна мелкая неприятность. Если по какой-то причине у нас есть узлы с неполными массивами, то мы не можем вставлять в крайние позиции массива, поскольку они ограничивают значения дочерних узлов, и подобная вставка собьёт ограничения. Чтобы всем было понятно, покажу не примере:


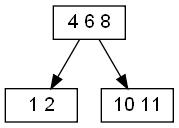
Мы хотим вставить в дерево число '9', в массиве корневого узла есть место, но вставить число в корневой узел мы не можем. Мы может вставить в корень числа '5' или '7', а появление '9' в корне, нарушит свойства бинарного дерева поиска. Проще говоря во время разнородных вставок и удалений из такого дерева, не узлы истощаются и пустеют, очень медленно, но безвозвтарно. Поэтому мы может либо на давать им истощаться слишком сильно, либо всегда держать их полными. В первом случае после удаления и возвращаем массив в полное состояние с помощью нового значения, подтянутого откуда-нибудь из листьев дерева.

Примеры

Итак, вариант первый, дерево которое всегда поддерживает массивы не листовых узлов полными. Поиск внутри массивов линейный:

Балансировка

Поскольку это дерево мало чем отличается от бинарного дерева поиска, то балансировать его можно только так же. Следить за высотой нелистовых деревьев и делать повороты, тупо переставляя местами узлы. При желании можно задействовать в поворотах листья, можно так же делать не перестановку узлов, а более тонкие повроты с сдвигом значений в некоторых узлах. Но всё это уже немного сложнее и абсолютно ненужно. Про балансировку узлов в бинарном дереве можно прочитать тут: [avl].

Есть методы менее эффективные, но более простые и практичные. Весь фокус в том что частично балансом можно управлять, меняя своё поведение во время вставки и удаления. Это можно сделать в двух местах:

  1. после удаления мы можем выбрать откуда заполнять неполный массив, из левой или правой ветки.
  2. после вставки в середину заполненного массива, мы можем выбрать какое из двух крайних чисел можно спихнуть вниз.
Эти фокусы разумеется не спасут нас в случае, если кто-то например засунет в дерево возрастающие числа, мы всё равно получим не дерево, а линейный список. А в целом, делая осмысленный выбор в этих двух ситуациях мы сильно облегчим себе работу. Для работы проще добавить в каждый узел счётчик дисбаланса. Причём считать он может не высоту веток, я разницу между количеством элементов в левом и правом поддереве. Образец прилагается:

Ещё одна, занятная стратегия балансировки заключается в том чтобы всё таки не поддерживать, узлы дерева полными, а востанавливать их наполненость в случае заметного истощения. Недостающие элементы массивов восполняются из листьев. Исходник с отложенной балансировкой прилагается:

Заключение

Вообще не несколько дней отвлёкся от этого текста, с тех пор как начал его писать, я даже забыл чего хотел написать в этоге. Могу заявить мимоходом что b-дерева эта конструкция не заменяет, особенно для хранения данных на диске; слишком слабое ветвление. Так в просто ещё раз повторю все сслыки, а так же дам ещё один вариант, в котором нет счётчика значений внутри узла, а есть значение зарезервированное как пустое:
Hosted by uCoz